上周，“袁来如此”专栏就大分(fēn)子生物(wù)分(fēn)析方法的校准曲線(xiàn)的设计、生成和编辑的思考和建议展开了详细介绍（袁来如此｜大分(fēn)子生物(wù)分(fēn)析概论（四_上）：校准曲線(xiàn)的设计，生成和编辑），本期将延续上期内容，重点介绍大分(fēn)子生物(wù)分(fēn)析方法校准曲線(xiàn)拟合模型和权重进行取舍的方法。

本系列文(wén)章介绍的生物(wù)分(fēn)析是指定量地测定在动物(wù)和人體(tǐ)體(tǐ)液或组织中的生物(wù)药（本文(wén)特指蛋白质类生物(wù)药，包括单抗，细胞因子，生長(cháng)素，融合蛋白等）的浓度。大多(duō)数生物(wù)分(fēn)析方法都基于免疫测试方法（Immunoassays），或者更广义地称為(wèi)，配體(tǐ)结合式测试方法（ligand binding assays, LBA）。这些方法涉及一系列试剂的使用(yòng)，如抗药物(wù)抗體(tǐ)，其它抗體(tǐ)，生物(wù)药的靶标蛋白等。

配體(tǐ)结合式测试方法（LBA，也称為(wèi)immunoassays）是一种常用(yòng)的定量分(fēn)析工具。在LBA方法中，待测物(wù)浓度与响应数据之间的关系是质量作用(yòng)定律驱动的非線(xiàn)性关系，两个被广泛接受和经过验证的LBA校准曲線(xiàn)的回归模型是4参数logistic（4PL）和5参数logistic（5PL）曲線(xiàn)拟合模型。选择适当的回归模型和权重函数是LBA方法开发的关键组成部分(fēn)。

在分(fēn)析方法开发期间，应对选定的模型和权重函数进行评估，并在验证期间加以确认。关于确定或选择适当的回归模型和权重函数的实际操作方法，在已发表的文(wén)献中颇為(wèi)有(yǒu)限，本文(wén)将提出一个结构化的、有(yǒu)序的方案来确定两者。

在LBA中观察到的实验响应是一个配體(tǐ)（待测物(wù)）和检测系统中使用(yòng)的特定捕获/检测试剂的平衡结合的结果。实验响应与对数变换后浓度之间的这种关系是非線(xiàn)性的，使得典型的LBA校准曲線(xiàn)為(wèi)全部或部分(fēn)的S型（sigmoidal）。常见的非線(xiàn)性回归模型為(wèi)4PL和5PL，拟合模型的选择可(kě)能(néng)由曲線(xiàn)的形状所驱动。完全的 sigmoidal曲線(xiàn)（其中顶部和底部平台區(qū)是镜像）通常使用(yòng)4PL 模型。部分(fēn)sigmoidal曲線(xiàn)，即非对称曲線(xiàn)，通常使用(yòng)5PL模型（4PL、5PL模型详细解读请戳《袁来如此｜大分(fēn)子生物(wù)分(fēn)析概论（四_上）：校准曲線(xiàn)的设计，生成和编辑》）。

由于LBA中配體(tǐ)平衡结合（equilibrium binding）的特性，经常会观察到测试响应的非恒定的方差（non-constant variance of response），这种不等同方差称為(wèi)异方差性（heteroscedasticity）。如果在曲線(xiàn)拟合时不考虑应对异方差性，则可(kě)能(néng)导致最终结果中出现回算错误和更大的偏差。為(wèi)了减少异方差性的影响并提高曲線(xiàn)拟合的质量，必须尽量减少具有(yǒu)较高方差（higher variance）的校准点对曲線(xiàn)拟合的贡献，广义最小(xiǎo)平方 （generalized least squares）和方差稳定变换（variance stabilizing transformation）可(kě)以用(yòng)来解决这个问题。这些方法要么在每个拟合迭代后更新(xīn)权重函数；要么转换数据和模型，以使用(yòng)普通最小(xiǎo)平方模型，而不使用(yòng)权重函数。在已发表的方法中，線(xiàn)性回归斜率方法（linear regression slope approach）可(kě)能(néng)是最实用(yòng)的。本文(wén)下面讨论这个方法。

大多(duō)数与 LBA测试相关的软件為(wèi)各种拟合模型和常用(yòng)的权重函数（如 1/Y 或 1/Y2）提供了内置的选择。相关监管指南建议使用(yòng)最简单，并充分(fēn)描述了待测物(wù)浓度与其响应之间关系的模型。在选择回归模型（加或不加权重）时，如果对曲線(xiàn)形状的目视评估和对使用(yòng)的统计方法进行比较，如比较F测试和chi-square p value，并不容易，其结果可(kě)能(néng)会令人困惑。这里常见的挑战是如何依据相关知识，合理(lǐ)地选择其中之一。

本文(wén)将介绍一组案例研究，其中采用(yòng)药代动力學(xué)定量分(fēn)析方法，用(yòng)于血清或血浆中蛋白生物(wù)药的定量，以及使用(yòng)通用(yòng)的统计软件来确定适当的拟合模型和权重因子。

LBA方法是评估生物(wù)药的PK/TK时的主要定量分(fēn)析方法，该方法的特异性和选择性取决于目标待测物(wù)与其他(tā)生物(wù)分(fēn)子（如受體(tǐ)、和针对候选生物(wù)药的抗體(tǐ)）的相互作用(yòng)。LBA方法中观察到的信号/响应与生物(wù)药的浓度间接相关。

下面的示例A、B和C都使用(yòng)了LBA方法，如電(diàn)化學(xué)发光（ECL）检测平台或比色法ELISA检测平台，用(yòng)于定量分(fēn)析血浆或血清（人或食蟹猴）中的蛋白生物(wù)药浓度。每个案例研究中的分(fēn)析方法简述如下：

案例A：对Meso Scale Discovery（MSD）Multi-Array®微孔板，使用(yòng)单克隆抗药物(wù)抗體(tǐ)（5 g/mL）包板，过夜；之后，与含有(yǒu)药物(wù)的样品在室温下孵育60分(fēn)钟；洗板后，结合到板上的药物(wù)与biotinylated单克隆检测抗體(tǐ)（2.5g/mL）孵育60分(fēn)钟；然后加入0.1g/mL 的Streptavidin-ruthenium，再孵育60分(fēn)钟；之后，MSD仪器在特定条件下检测到来自ruthenium 的電(diàn)化學(xué)发光信号。

案例B：对streptavidin 包被的MSD Multi-Array®微孔板，在室温下，以biotinylated单克隆抗體(tǐ)（4mg/mL）包板60至120分(fēn)钟；随后，含有(yǒu)药物(wù)的样品在上述微孔板上孵育90分(fēn)钟；使用(yòng)小(xiǎo)鼠抗人IgG Fc-Ruthenium（0.36mg/mL）孵育60分(fēn)钟，以结合被抗體(tǐ)捕获的生物(wù)药；之后，MSD仪器在特定条件下检测到来自ruthenium 的電(diàn)化學(xué)发光信号。

案例C：在Costar微孔板上，在4°C包被药物(wù)靶点（4 mg/mL），过夜；与靶点结合后的生物(wù)药，再与50 ng/mL的biotinylated单克隆抗體(tǐ)孵育60分(fēn)钟；之后，再与1:50,000稀释后的avidin D-HRP 孵育60分(fēn)钟；随后，加入HRP酶底物(wù)，TMB，以产生色度反应；然后用(yòng)硫酸停止该反应，并在酶标仪Spectramax上，测量450nm的光學(xué)密度（OD）。

异方差性（Heteroscedasticity）

在采集到的实验运行的标准校准数据集合（standard calibration data）中，可(kě)以通过观察测试信号的标准偏差（SD）和校准点浓度之间的关系来评估异方差性。為(wèi)此，分(fēn)别评估了案例A、B和C在方法开发过程中获得的6、7和10个独立运行。

首先，使用(yòng)Microsoft Excel 2010计算标准方差，其次使用(yòng) GraphPad Prizm 7 来绘制每个校准品测试信号的SD与校准点浓度的关系图。在目视考查了SD变化的趋势后，就可(kě)以确定对权重函数的需求。如果SD发生移动，则表明了异方差性，因此，需要使用(yòng)权重函数。如果SD在校准品浓度范围内是恒定的，则无需加权。

当在校准曲線(xiàn)中观察到测试信号的标准偏差随浓度发生变化时，就需要对更精确的数据点（具有(yǒu)较低SD的数据）使用(yòng)权重函数来调整曲線(xiàn)的拟合。在 GraphPad Prizm 7 中，可(kě)以使用(yòng)图形線(xiàn)性回归方法（graphical linear regression approach）计算权重函数因子如下：

步骤1. 绘制下述二者的关系图：对数转换后的测试信号平均值与对数转换后的SD，对二者使用(yòng)相同的对数底数（10或2）。

步骤2. 在步骤1中得到的線(xiàn)性回归直線(xiàn)的斜率值（k）乘以2，以确定权重函数因子（weighting function factor），即2k。

為(wèi)了平衡所有(yǒu)校准点的贡献，在4PL或5PL曲線(xiàn)拟合中应用(yòng)权重函数 1/Y2k（其中Y是测试信号，2k是权重因子），以尽量减少weighted sum-of-squares，从而获得更好的准确度和精密度。

将权重函数 1/Y2k 应用(yòng)于曲線(xiàn)拟合模型 （4PL 或 5PL）后，再使用(yòng)Watson LIMS，将回算的校准点浓度插入加权拟合的曲線(xiàn)（假定这些校准点是未知浓度的样本）。

如果对所有(yǒu)测试运行和对每个标准校准点（锚定点除外），累积%RE在±15% 之内并且累积%CV≤15%，则回归模型是可(kě)以接受的；但对于定量下限（LLOQ）和上限（ULOQ），接受标准一般 %RE±20和累积 %CV≤20。估计的定量范围（ROQ）是在符合上述接受标准的最低和最高标准浓度之间确定的。在 MS  Excel 2010 中，累计%RE和累积%CV 分(fēn)别计算為(wèi)：[100 - 100 x（回算浓度的平均值/标称浓度）]和 100 X（回算浓度的标准方差/回算浓度的平均值）。

之后，使用(yòng) GraphPad Prizm 7 绘制 4PL 和 5PL 之间准确度（累积cumulative %RE）和精密度（累积cumulative %CV）的比较图。回归模型的适宜性可(kě)使用(yòng)此可(kě)视化图形工具来判断：在可(kě)接受的范围内包含了更多(duō)标准校准点，而且累积 %RE 和累积 %CV 较低模型，就是应该选择的模型。如果两种模型的效能(néng)非常相似，则可(kě)通过是否具有(yǒu)加权4PL来做选择 ，因為(wèi)一般遵循 Occam’s razor 原则， 即以最少的假设，发现数据和模型之间的关系。

图1. 选择曲線(xiàn)拟合模型以提高曲線(xiàn)性能(néng)的方法。实际工作流程描述了选择权重函数和曲線(xiàn)拟合模型的每个步骤和整个过程。

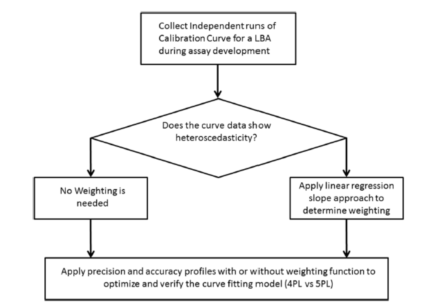
本文(wén)提出了一种结构化的方法，通过选择正确的曲線(xiàn)拟合模型和权重函数，以扩展 LBA分(fēn)析方法的定量范围（图1）。该方法完全从数學(xué)的角度出发，确定一条校准曲線(xiàn)是否需要加权重以及哪种加权方式最合理(lǐ)。如果收集到的数据中呈现出的异质性，则在准确度和精密度行為(wèi)方面，对4PL和5PL两个模型（以及确定的权重函数）进行比较；如果未观察到异方差性，则对不含权重量4PL和5PL模型进行比较。以下将此原则应用(yòng)于3个典型 LBA分(fēn)析案例。在这3个生物(wù)药的药代动力學(xué)（PK）研究案例中，总共开发了3个分(fēn)析方法，并观察到3种不同形状的校准曲線(xiàn)。其中，两个分(fēn)析方法（案例A和B）利用(yòng)了電(diàn)化學(xué)发光（ECL）平台，而另一个分(fēn)析方法（案例C）使用(yòng)了比色ELISA平台。

為(wèi)了在方法开发过程中对浓度-测试信号的关系进行详细研究，表1中描述了定量分(fēn)析生物(wù)药A、B和C浓度的3条校准曲線(xiàn)。在预期的定量范围内（对数尺度上），校准点大致均匀分(fēn)布。

表1. 3条PK校准曲線(xiàn)的特征总结

用(yòng)于评估各自PK分(fēn)析运行的校准曲線(xiàn)数据如图2所示。在所有(yǒu)3个案例研究中都观察到了典型的非線(xiàn)性的浓度-响应曲線(xiàn)。

图2. 3个案例研究中的校准曲線(xiàn)：案例 A（a），案例 B（b） 和案例 C（c）。该图展示了3条标准曲線(xiàn)的形状，代表了在LBA测试中通常观察到的典型非線(xiàn)性响应。X轴代表校准点浓度的对数，Y轴代表响应读数：案例A和B是相对光单位（RLU），案例C是450 nM 光學(xué)密度（OD 450）。

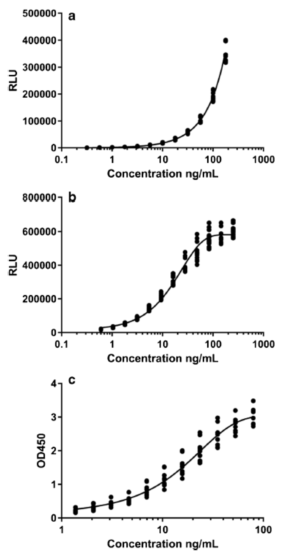
图3. 案例A（a）、案例B（b）和案例C（c）的异方差性概况。X轴代表校准点浓度的对数，Y轴代表实验运行中测试信号的SD。

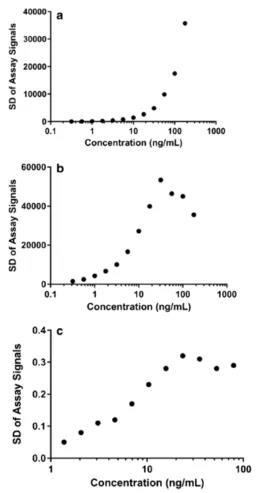
下面评估了表1中3条校准曲線(xiàn)上测试信号的标准偏差（SD），该SD是异方差性的直接指标。这3条校准曲線(xiàn)上测试信号的SD（变异性variability）不是恒定的，而是随着校准点的浓度而改变化的（图3）。

对于案例A，当药物(wù)浓度超过 20 ng/mL时，其变异性急剧增加。在案例B中，SD大幅增加，直到48.3 ng/mL的浓度，并在 48.3和 250 ng/mL 之间出现下降趋势。对于案例C ，SD 增加，一直到23.5 ng/mL的浓度，之后稍微降，直至79.3 ng/mL。总體(tǐ)而言，浓度较高校准点的SD大于浓度较低校准点。校准曲線(xiàn)之间的非恒定 SD 模式代表示异方差性，在较高浓度下的高变异性表明需要使用(yòng)加权拟合。图1所示的决策树指明了如何确定适当的权重因子和可(kě)以接受的拟合模型。

為(wèi)了确定权重因子，首先需要从下面的線(xiàn)性回归中得出斜率（k值）：对数变换的测试信号SD vs 对数变的换测试信号平均值（图4）；然后，应用(yòng) 1/Y2k 方程式来计算最终的权重函数。对于案例 A，B 和 C，線(xiàn)性回归的斜率分(fēn)别為(wèi) 1.06、1.00 和 0.657。对于案例 A 和 B，由于斜率接近1.0，因此在4PL和5PL模型中使用(yòng)了权重函数1/Y2 。对于 C 例，权重函数為(wèi) 1/Y，由于斜率接近 0.5。在Waston LIMS中，只有(yǒu) 1/Y or 1/Y2这两种权重函数可(kě)用(yòng)。

图4. 案例 A（a）、案例 B （b） 和案例 C （c）中k值的确定。案例 A、B 和 C 的斜率（k值）分(fēn)别為(wèi) 1.06、1.00 和 0.657。案例A、B和C的R2（确定系数coefficient of determination）分(fēn)别為(wèi)0.998、0.984和0.934。

為(wèi)确定可(kě)以接受的曲線(xiàn)拟合模型，考察了如下参数：4PL和 5PL模型；权重函数：1/Y2（案例A），1/Y2（案例B）和 1/Y（案例C）；比较参数：回算浓度的累积 %RE（图5）和累积 %CV（图6）。应当选择在可(kě)接受的范围内，具有(yǒu)较低的%CV和%RE校准点数量较多(duō)的回归模型。如果两者都是相当的，则应选取加权4PL作為(wèi)最终的曲線(xiàn)拟合模型。在 Watson LIMS 中生成每次运行的回算浓度。所有(yǒu)情况的回算浓度的累积 %RE和 %CV计算（在曲線(xiàn)拟合模型确定章节的 B 部分(fēn)）。图5和图6给出了加权4PL模型与加权5PL模型的累积 %RE和累积 %CV的比较。

如图5所示，对于具有(yǒu)相应权重函数的4PL和5PL模型，所有(yǒu)校准点的 %RE分(fēn)别：案例A， 低于4%和3%；案例 B，低于18%和16%；案例 C，低于7 和 6%。在所有(yǒu)案例研究中，加权4PL和加权5PL模型的准确度是相当的，对于案例 A、B 和 C，所有(yǒu)校准点都在可(kě)以接受的范围内。根据准确度行為(wèi)图推断的定量范围（ROQ）分(fēn)别為(wèi)：0.317-178 ng/mL（案例A），0.602-250 ng/mL（案例B），和1.37-79.3 ng/mL（案例C）。

图5. 准确度行為(wèi)图。对案例A（a）、案例B（b）和案例C（c）中校准曲線(xiàn)的加权（1/Y或者1/Y2）拟合模型进行了比较。比较模型：4PL vs 5PL；比较参数：回算浓度的累积相对误差（%RE）。两条虚線(xiàn)之间的區(qū)域是可(kě)接受范围（± 20%）。（○）代表4PL加权拟合，（□）代表5PL加权拟合。

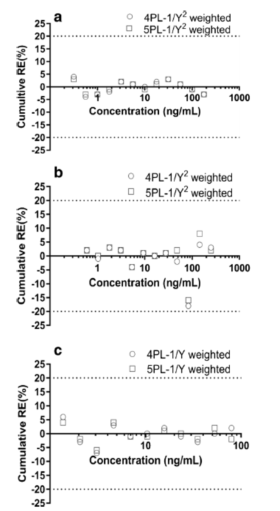
图6显示，对于加权4PL和加权5PL曲線(xiàn)拟合模型，所有(yǒu)校准点的累计%CV：案例A，低于3.0和2.9%；案例B，低于39.7%和26.3%；案例C，低于6.6%和10.8%。案例A和C对两个拟合模型加权拟合后，所有(yǒu)校准点的 %CV变得相当了。对案例A和C，所有(yǒu)校准点的加权4PL和加权5PL的精密度也是相似的。根据精密度行為(wèi)图推断的ROQ分(fēn)别為(wèi)0.317-178 ng/mL（案例A）和1.37-79.3 ng/mL（案例C）。使用(yòng)加权4PL模型，与加权5PL模型相比，案例B可(kě)以接受的校准点数量从9增加到11，加权4PL模型的估算的ROQ 為(wèi) 0.602-145 ng/mL，而加权5PL模型的检测范围较窄：0.602 - 48.3 ng/mL。根据接受标准，对于案例 A、B 和 C ，最终可(kě)以接受的曲線(xiàn)拟合模型都是4PL，权重函数分(fēn)别為(wèi) 1/Y2，1/Y2和1/Y。

图6. 精密度行為(wèi)图：案例A（a），案例B（b）和案例C（c）比较模型：加权4PL vs 加权5PL；比较参数：回算浓度的 %CV。虚線(xiàn)和X轴之间的區(qū)域是可(kě)接受范围（± 20%）。（○）代表 4PL 加权拟合，（□）代表 5PL 加权拟合。

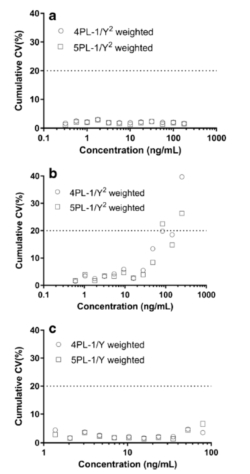
图7演示了对案例 A 应用(yòng)上述方案后，校准曲線(xiàn)性能(néng)是如何改进的（此处不显示案例B和C的图表）。使用(yòng)非加权4PL回归模型回算浓度绘制的准确度行為(wèi)图（累积 %RE，图7a）表明，与加权相比此模型表现出更窄的动态范围，0.563-178 ng/mL；加权4PL模型：0.317-178 ng/mL。非加权 5PL回归模型显示更好的准确度：所有(yǒu)校准点低于20%。但是，在应用(yòng)1/Y2的权重函数（在“异方差度评估”章节确定）后， 所有(yǒu)校准点的累积 %RE得到改善，都在±3%以内（图7a）。

精密度行為(wèi)图（累积 %CV，图7b）显示，非加权4PL和5PL回归模型的ROQ显著狭窄：1.00-178 ng/mL；而在使用(yòng)了1/Y2 的权重函数后，ROQ变為(wèi)0.317-178 ng/mL。该校准曲線(xiàn)低端的效能(néng)的显著改善显示了加权拟合的力量，因其降低了高变异性的测试信号对曲線(xiàn)拟合的影响。案例A表明，使用(yòng)适当的权重函数可(kě)以提高精密度和准确度（均低于4%）以及扩展定量范围（0.317-178 ng/mL）。

图7. 案例A标准曲線(xiàn)加权之前和之后，4PL和5PL模型的准确度和精密度行為(wèi)图。累积 %RE（图 7a）和累计 %CV（图7b）在模型之间的比较：4PL vs. 5PL（无权重）；以及4PL vs. 5PL（权重因子：1/Y2）。

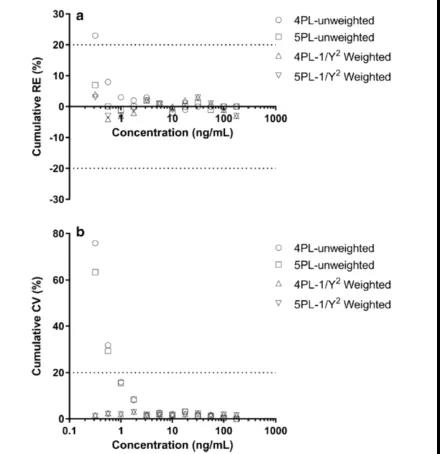
表2显示，使用(yòng)适当的权重函数可(kě)以扩展ROQ。对案例B，应用(yòng)权重函数到4PL回归模型后，ROQ得到显著扩展；从未加权的1.04-48.3 ng/mL到 加权的0.602-145 ng/mL；加权5PL模型的ROQ，则从未加权1.04-145 ng/mL变為(wèi)加权的0.602-48.3 ng/mL。对案例C，4PL模型的ROQ略有(yǒu)扩展：从未加权的2.06-79.3 ng/mL，到加权的1.37-79.3 ng/mL。对于5PL模型，使用(yòng)权重函数后ROQ没有(yǒu)增加。

本文(wén)為(wèi)确定LBA定量分(fēn)析方法中校准曲線(xiàn)的回归模型及权重函数的选择，提供了一个决策树和相应的方法，目的是為(wèi)了為(wèi)减少异方差性（heteroscedasticity）的影响。本文(wén)的建议得到3个案例研究的支持。

由于LBA中平衡结合（equilibrium binding）的特性，实践中经常观察到测试响应的非恒定方差，称為(wèi)异方差性（heteroscedasticity）。本文(wén)发现線(xiàn)性回归斜率方法（linear regression slope approach）是解决异方差性最实际的方法。

在方法开发过程中，可(kě)以绘制校准曲線(xiàn)的测试信号的标准方差（standard deviation，SD）与校准点浓度的对数的相关图。一条校准曲線(xiàn)的非恒定SD趋势表明存在异方差性，这意味着需要使用(yòng)权重函数。所有(yǒu)的3个案例研究（A，B 和 C）都显示，测试信号在较高药物(wù)浓度下，具有(yǒu)更高的变异性，需要加权拟合校准曲線(xiàn)。一般而言，任何一个LBA定量分(fēn)析方法，都会受益于使用(yòng)权重函数。

需要注意的是，一旦确定需要权重因子，如何确定正确的权重因子则成為(wèi)重中之重。本文(wén)推荐的方法是：首先，从测试信号（Y）的标准方差（对数变换后）与测试信号平均值（对数变换后）的線(xiàn)性回归关系中，确定其斜率，又(yòu)称k值；然后，将斜率（k） 代入以下方程 1/Y2k 中，以确定权重因子（1/Y 或 1/Y2）。

在案例研究 A、B、C 中，線(xiàn)性回归的斜率分(fēn)别為(wèi) 1.06，1.00 和 0.657; 因此，权重因子分(fēn)别估计為(wèi)2，2和1。在案例A和B中，权重因子為(wèi)2; 因此，在校准曲線(xiàn)回归模型（4PL或5PL）中，使用(yòng)了权重函数1/Y2。对于案例C，权重系数為(wèi) 1; 因此，权重函数為(wèi) 1/Y。

為(wèi)了确定可(kě)接受的曲線(xiàn)拟合模型，应评估拟合曲線(xiàn)的4PL与5PL模型（不加权和加权）回算浓度的累积 %RE和累积 %CV。应当选择，在可(kě)接受的范围内，具有(yǒu)较低的%CV和%RE，校准点数量较多(duō)的回归模型。如果两者都是相当的，则选择加权4PL模型作為(wèi)最终曲線(xiàn)拟合模型，进行方法验证和样本分(fēn)析。根据 FDA 指南，应当选择假设最少的模型，即选择最简单的模型。根据精密度和准确度数据，在所有(yǒu)3个案例中，4PL都是基于这些标准的最佳回归模型。

為(wèi)了验证所选择回归模型和权重函数，可(kě)以做其他(tā)评估。例如，在使用(yòng)权重函数之前和之后，可(kě)以比较4PL和5PL模型的准确度和精密度行為(wèi)。本文(wén)给出了4PL与5PL（无加权和 1/Y2加权）的累积 %CV 和累积 %RE 的比较，累积 %RE的可(kě)接受范围為(wèi)± 20%，累积 %CV 的可(kě)接受范围為(wèi)≤20%。

案例A表明，使用(yòng)适当的权重函数可(kě)以提高精密度和准确性（均低于10%）和扩展定量范围（0.317-178 ng/mL）。在案例B和C中，校准曲線(xiàn)拟合也有(yǒu)改善。案例B在4PL回归模型上加权后，ROQ得到显著扩展：未加权时為(wèi)1.04-48.3 ng/mL；加权后為(wèi) 0.602-145 ng/mL；5PL模型，未加权1.04-145 ng/mL，加权后0.602-48.3 ng/mL。案例C4PL模型在加权后ROQ 略有(yǒu)扩展：未加权2.06-79.3 ng/mL；加权為(wèi)1.37-79.3 ng/mL。

在定量 LBA 方法开发过程中，本文(wén)介绍了一个简单、易于使用(yòng)的决策树，以确定校准曲線(xiàn)的最佳回归模型和权重。所推荐的方法将选择一个加权的曲線(xiàn)拟合模型。

1. 在方法开发过程中，至少需要使用(yòng)3个独立的测试运行对模型选择进行初步评估; 但是，一般建议增加运行的数量，以便在研究前验证时，验证曲線(xiàn)拟合模型。由于对响应-误差关系的估计存在局限性，因此不建议使用(yòng)较小(xiǎo)的数据集合；

2. 评估异方差性；

3. 如果存在异方差性，就通过斜率方法确k值（即斜率），然后计算权重因子（权重函数=1/Y2k）；

4. 使用(yòng)准确度（%RE）和精密度（%CV）行為(wèi)来选择和验证更好的加权回归模型；

5. 建议使用(yòng)独立制备的质量控制样品（QC）来验证分(fēn)析方法的定量范围。

本文(wén)如有(yǒu)疏漏和误读相关指南和数据的地方，请读者评论和指正。所有(yǒu)引用(yòng)的原始信息和资料均来自已经发表學(xué)术期刊, 官方网络报道, 等公开渠道, 不涉及任何保密信息。参考文(wén)献的选择考虑到多(duō)样化但也不可(kě)能(néng)完备。欢迎读者提供有(yǒu)价值的文(wén)献及其评估。